StyleGAN 논문 리뷰
StyleGAN Review
1. Intro
GAN으로 생성된 이미지의 해상도나 퀄리티는 지속적으로 발전을 이루어 왔습니다. 하지만 Generator의 한계가 아직도 명확하게 존재하였습니다. Generator가 black boxes로 여겨졌으며 이미지 합성과정의 대한 이해와 latent space에 대한 이해가 부족했기 때문입니다. 또한 서로 다른 Generators에 대한 비교 역시 어려웠다는 한계점도 존재했습니다. 따라서 본 논문은 새로운 Generator를 도입하여 위와 같은 문제점들을 해결하고자 하였습니다.
본 논문의 모델의 경우 constant input을 넣고 이미지의 ‘style’을 각 convolution layer마다 latent code를 통해 적용하는 과정을 거치게 됩니다. 따라서 서로 다른 scale에서의 조절을 가능하게 하였습니다. 또한 noise를 network에 직접적으로 넣으면서 unsupervised하게 자동적으로 high-level 특성들(pose, identity 등)과 stochastic variation의 구분이 가능하도록 조절하였습니다. 이때 Discriminator와 loss function은 그대로 둔채 Generator의 모델만 바꿔 좋은 퀄리티의 이미지를 생성했다고 할 수 있겠습니다. 모델의 경우 뒤에서 조금 더 자세히 살펴보겠습니다.
마지막으로 본 논문에서 새로운 사람 얼굴 데이터, Flickr-Faces-HQ(FFHQ)를 제시하였습니다. 이전 데이터들보다 더 높은 퀄리티의 고화질 이미지를 보유하고 있으며 더 넓은 다양성을 가지고 있다고 합니다.
2. Architecture
2-1. Generator
기존 GAN들의 Generator를 한 번 생각해보세요. Latent code $z$가 아래의 왼쪽 그림처럼 input layer로 바로 들어왔던 것을 떠올릴 수 있을 것입니다. Input layer로 들어온 $z$가 Generator의 여러 layer들을 통과하게 되면 하나의 이미지가 생성되었습니다. 하지만 본 논문에서 새롭게 제시하는 Generator의 모습은 input layer로 들어온 $z$가 아닌 constant에서 시작됩니다. 아래의 오른쪽 모델처럼 Latent space $\mathcal{Z}$가 여덟 개의 MLP로 이루어진 $f$ mapping를 통과해 $\mathcal{W}$가 만들어지고 $\mathcal{W}$를 통해 이 Generator의 convolution layer 사이사이 style이 들어가는 형태를 보여줍니다. 이때 Adaptive instance normalization(이하 AdaIN)을 사용하게 됩니다. 또한 Noise가 AdaIN이 적용되기 이전에 들어가는 모습 역시 확인할 수 있습니다.
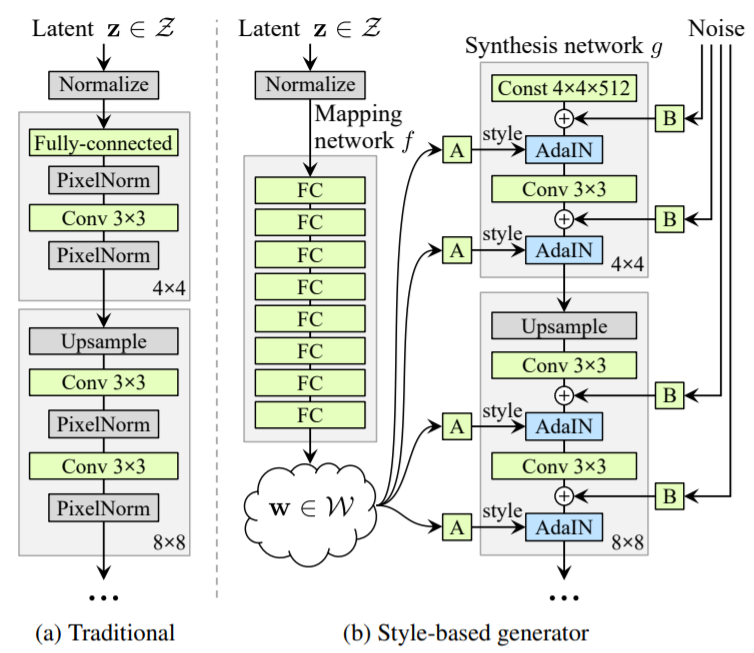
이러한 $\mathcal{W}$를 활용하는 형태의 Generator를 사용하는 것은 기존의 Generator의 경우 training data의 분포를 따라하기 때문에 linear하지 않고 entangled된 distribution을 보여줄 수 있기 때문입니다. 본 논문에서는 이를 unavoidable entanglement라고 표현하고 있습니다. (b)처럼 별도의 mapping network를 만들게 되면서 latent space가 제한에서 벗어나게 되고 disentangled됩니다.
2-2. AdaIN
그렇다면 Generator에서 style을 집어넣을 수 있는 방법인 AdaIN 무엇일까요? AdaIN은 채널마다 평균 0, 단위분산이 되도록 normalize를 진행하고 이후 스타일을 바탕으로 스케일과 bias를 적용하는 방법입니다. 식은 아래와 같습니다. $x_i$는 각 feature map을 말하며 $y_{s,i}$와 $y_{b,i}$는 affine transforms를 통해 $w$를 변환시킨 값입니다. 간단하게 생각하면 normalization 후 스타일을 넣어주는 과정이라고 보면 될 것 같습니다. \(AdaIN(x_i, y) = y_{s,i} \frac{x_i-\mu(x_i)}{\sigma(x_i)} + y_{b,i}\) AdaIN은 간결한 표현과 효율성 때문에 사용을 하게 되었다고 합니다.
2-3. Final Architecture
- Baseline: Progressinve GAN
- Bilinear up/downsampling, longer training, tuned hyperparameters
- Add mapping network and AdaIN
- Remove traditional input
- Add noise
- Mixing regularization
3. Experiments and Results
3-1. Ablation Studies
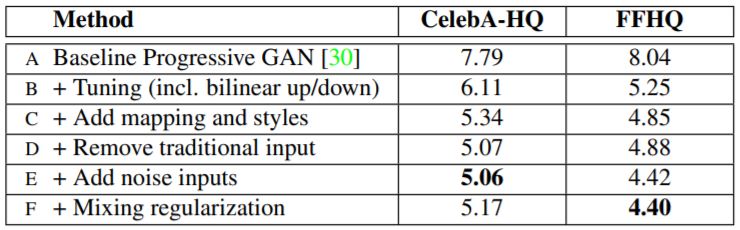
Baseline인 Progressive GAN에서 조금씩 StyleGAN에 필요한 과정들을 추가하면서 Frechet inception distance(FID)결과를 살펴본 결과 tuning, mapping layers, remove traditional input, add noise를 추가했을때 점점 성능이 좋아지는 것을 확인할 수 있었습니다. FFHQ의 경우 mixing regularization을 해주면 성능은 더욱 상승하였습니다. 정리해보면 처음의 Traditional Generator와 Style-based Generator(E)를 비교하게 되면 약 20%의 성능향상이 있었습니다.
3-2. Properties of the Style-based Generator
Style mixing
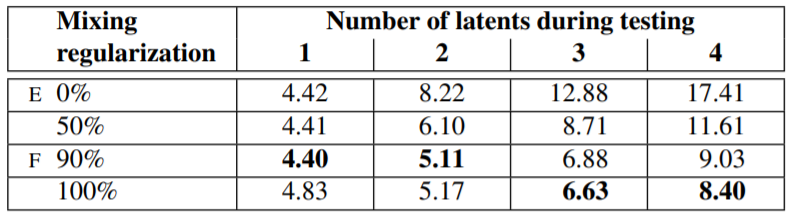
위에서 잠깐 언급한 mixing regularization의 경우 두 가지의 랜덤한 latent codes를 training에서 사용하는 것을 말합니다. 이를 style mixing 과정이라고 저자는 소개하고 있습니다. 방법은 다음과 같습니다. 하나가 아닌 두 가지의 latent code $z_1$, $z_2$를 모두 mapping network에 통과시켜 $w_1$과 $w_2$를 얻습니다. 이때 특정 layer는 $w_1$, 나머지는 $w_2$를 사용하여 training을 진행합니다. 이 방법은 인접한 스타일들이 correlate되는 것을 막기 위한 목적이라고 합니다. 그 결과는 위의 표와 같습니다. Mixing regularization을 적절히 사용했을때 좋은 성능을 보여주는 것을 확인할 수 있습니다.

생성된 이미지들을 살펴보겠습니다. 위의 이미지는 source B의 일부 스타일을 적용하고 나머지는 모두 source A를 적용한 모습입니다. Source B를 $(4^2-8^2)$, 즉 layer 앞단에 적용했을 때는 포즈, 얼굴모양, 안경, 전반적인 헤어스타일 등의 high-level aspects가 source B를 따르고 나머지 특성들은 A를 따르는 것을 확인할 수 있었습니다. Source B를 중간 단계인 $(16^2-32^2)$에 넣었을 때는 좀 더 작은 범위의 얼굴특성들과 헤어스타일이 B를 따랐으며 $(64^2-1024^2)$에 넣었을 때는 color scheme과 microstructure가 B를 따르는 것을 알 수 있었습니다.
Stochastic variation
Stochastic한 변화들에 대해서도 한 번 결과를 살펴보겠습니다. 여기서 말하는 stochastic한 특성들이란 style보다는 약간 범위가 작은, 즉 주근깨, 머리모양, 모공 등의 위치처럼 상대적으로 더 사소하다고 말할 수 있는 특징들을 말합니다. Noise에 따른 결과를 한 번 살펴보면 아래의 그림처럼 이미지의 스타일은 유지되지만 머리의 모양이 조금씩 달라지는 것을 확인할 수 있었습니다.

또 다른 예시를 살펴보면 아래의 (a)는 모든 layer에 noise를 삽입한 결과, (b)는 noise를 넣지 않은 결과, (c)는 뒷단의 layer에 noise를 적용한 경우 (d)는 앞단에 noise를 적용한 경우 입니다. 전반적인 스타일은 유지되지만 머리의 모양이 noise에 따라서 약간 바뀌는 것을 확인할 수 있습니다.

Separation of global effects from stochasticity
-
Change in style - Global effects
-
Noise - Stochastic variation
How?
- AdaIN을 통해 style의 정보를 담는 scale과 bias가 사용
- noise가 독립적으로 들어가면서 조절 가능
- 만약 그 반대의 상황이 발생하려고 한다면 Discriminator가 penalize하면서 조절
3-3. Disentanglement Studies
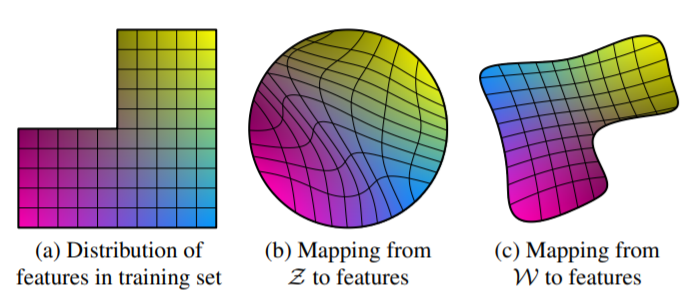
Disentanglement란 단어 의미에서도 알 수 있듯이 뒤틀리지 않는 것을 말합니다. 즉 아래 그림의 (a) 직선들처럼 변화의 한 부분씩을 담당하고 있는 linear subspaces가 있고 이 subspaces를 포함하는 latent space를 갖는 것이 목표라고 할 수 있습니다. 하지만 기존의 Generator처럼 $\mathcal{Z}$를 직접적으로 사용한다면 training data의 분포를 매칭해야하기 때문에 (b)의 휘어진 선들처럼 entangle하게 됩니다. 반면 본 논문의 모델은 $\mathcal{W}$가 고정된 분포를 따라서 sampling할 필요가 없기 때문에 (c)의 그림처럼 대체로 variation factors들이 linear한 모습을 띄는 것을 확인할 수 있었습니다.
아래의 그림에 대해서 조금 더 이야기를 해보자면 (a)는 masculinity와 hair length라는 두 가지의 variation factors를 표현한 것으로 이때 긴 머리를 가진 남성의 샘플이 존재하지 않는 data입니다. (b)의 경우 긴 머리를 가진 남성의 샘플이 training data에 없기때문에 고정된 분포에 맞추기 위하여 그 부분이 아예 사라지면서 휘어진 모습을 볼 수 있습니다. 반면 (c)의 경우 적절한 변형으로 학습이 이루어지게 됩니다.
그 정도를 측정하기 위해서는 기존과는 다른 척도가 필요한데 그 이유는 StyleGAN의 경우 기존 척도에 필요한 encoder의 구조를 가지고 있지 않기 때문입니다. 따라서 본 논문은 disentanglement를 측정할수 있는 두 가지의 척도를 제시하였습니다.(Perceptual path length, Linear separability)
Perceptual path length
Perceptual path length는 latent space를 interpolation하는 과정에서 이미지가 얼마나 급격하게 변하는지에 대해서 측정하는 척도입니다. 직관적으로 생각했을때 latent space의 휘어짐이 적을때 더 부드럽게 변화가 일어날 것임을 예측할 수 있습니다. 본 척도를 계산하기 위해서 학습된 VGG16에 이미지를 넣어 임베딩 시킨 후 임베딩 된 결과물들을 통해 perceptual difference를 구하게 됩니다.
이를 식으로 나타내면 아래와 같습니다. $l_{\mathcal{Z}}$과 $l_{\mathcal{W}}$는 각각 $\mathcal{Z}$와 $\mathcal{W}$의 각각 평균적인 perceptual path length를 나타냅니다.
-
$z_1, z_2 \sim P(z), t \sim U(0,1), \epsilon=10^{-4}$
- G = Generator, $g \circ f$ = style-based network, d($\cdot$,$\cdot$) = perceptual distance between the resulting images
- slerp = spherical interpolation, lerp = linear interpolation
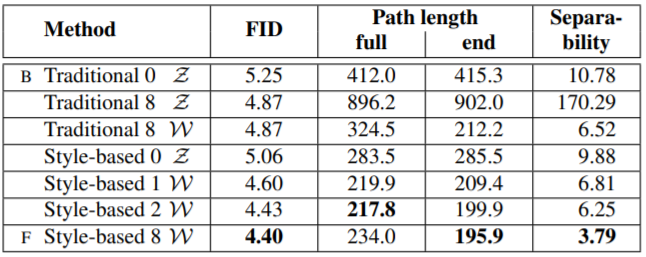
먼저 아래의 표 중 첫번째를 보게 되면 style-based generator와 noise를 사용한 모델, 즉 본 논문이 새롭게 제시하는 모델이 path length가 짧은 것을 확인할 수 있었습니다. 두번째 표를 살펴보면 기존의 모델과 새로운 모델 모두 mapping network가 있을때 성능이 좋았고 그 깊이가 깊을 때 perceptual path length와 FID 모두 개선이 이루어졌습니다. 또한 기존 모델에서 $\mathcal{Z}$를 사용하면 layer가 깊어져도 오히려 성능이 악화되는 결과를 보여주는 것으로 보아 latent space가 entangle 되었음을 확인할 수 있었습니다.
Linear separability
만약 disentanglement가 잘 이루어졌다면 각각의 variation factors에 대한 방향 벡터들을 찾을 수 있을 것입니다. 이를 활용한 척도가 linear separability로 linear hyperplane으로 얼마나 latent space 점들이 두 부분으로 분리될 수 있는지에 대한 척도입니다. $X$는 SVM에 의해서 예측된 클래스들, $Y$는 pretrained된 classifier에 의해서 결정된 클래스들이라고 할때 conditional entropy $H(Y \mid X)$를 통해서 실제 클래스를 결정하기 위해 얼마나 더 정보가 필요한지를 보여주는 것으로 이를 활용해 결과를 도출해낼 수 있습니다. 따라서 최종적인 식은 $exp(\sum_i H(Y_i \mid X_i))$이 됩니다. 이때의 $i$는 40개의 attributes에 대해서 진행하였습니다.
아래의 결과들을 살펴보면 $\mathcal{W}$를 사용하는 것이 더 분리를 잘 해내는 것을 알 수 있었고 그때의 mapping network가 깊을수록 더 좋은 결과를 보여주었습니다. 또한 기존의 Generator의 input layer 앞에 mapping network를 추가한 경우 separability는 좋지 못했지만 FID가 증가하는 것을 알 수 있었는데 training data를 따를 필요가 없는 것이 결과의 향상을 보여준 것이라고 합니다.