Self-Attention GAN 논문 리뷰
Self-Attention GAN Review
1. Intro
GAN이 처음 등장한 이후 많은 GAN 모델들이 나오게 되었습니다. 하지만 convolutional GAN들의 경우 multi-class 데이터셋에 대해서 학습을 진행하였을때 기하학적 혹은 구조적 패턴을 파악하지 못하여 이미지 클래스에 대한 모델링이 어렵다는 단점이 있습니다. 기존의 convolutional 필터의 경우 로컬한 정보들에 대해서는 잘 처리하지만 좀 더 큰 구조들에 대해서는 receptive fields가 커버하기 힘들기 때문입니다. 그렇다면 필터의 크기를 충분히 늘리면 되지 않을까하는 의문이 제기될 수 있습니다. 하지만 필터의 크기를 늘리게 된다면 계산적으로 효율성이 많이 떨어지기 때문에 학습에 어려움이 생길 수 있습니다.
따라서 Self-attention GAN(이하 SAGAN)은 그 이름에서도 알 수 있듯이 앞서 언급한 문제점들을 해결하고자 self-attention 개념을 응용해 효과적으로 이미지를 생성할 수 있도록 고안되었습니다. 아래의 그림처럼 SAGAN은 self-attention 방법을 사용하여 generator가 모든 위치에서 거리가 있는 부분까지 조화된 이미지를 만들 수 있게 되며 discriminator가 이미지 구조에 기하학적인 제약을 가할 수 있도록 해줍니다. Self-attention뿐만 아니라 SAGAN은 안정적인 학습을 위하여 추가적인 조건들을 사용하였는데 이는 뒤에서 말씀드리겠습니다.

2. Architecture
2-1. Self-attention to the GAN
먼저 SAGAN 모델의 가장 핵심이라고 할 수 있는 attention module에 대해서 설명드리겠습니다. 이 attention module은 generator와 discriminator 모두에 활용되는 구조로서 그림 2와 같은 형태를 띄고 있습니다.
Attention module은 convolution feature maps $x$가 input으로 들어오면서 시작이 됩니다. 이전 hidden layer의 이미지 features, $x$가 $f(x)=W_fx$와 $g(x)=W_gx$를 통하여 두 가지 feature spaces $f$와 $g$에 transform됩니다. 이러한 방식으로 만들어지는 값 $f(x)$와 $g(x)$를 행렬의 transpose를 적절하게 이용해 계산을 하게되면 $\beta_{j,i}=\frac{exp(s_{ij})}{\sum^N_{i=1}exp(s_{ij})}$, $s_{ij}=f(x_i)^Tg(x_j)$와 같은 식들이 도출됩니다. $s_{ij}$의 경우 $f$, $g$ 두 feature spaces를 행렬곱으로 계산한 값이며 $\beta_{j,i}$의 경우 구한 $s_{ij}$들을 softmax 계산식에 넣은 결과값들입니다. 아래의 구조도를 살펴보면 구한 $\beta_{j,i}$값은 attention map이라고 볼 수 있겠습니다. 좀 더 쉽게 풀어쓰면 location i가 location j를 표현할때 미치는 영향을 설명하는 것이라고 생각하시면 될 것 같습니다.
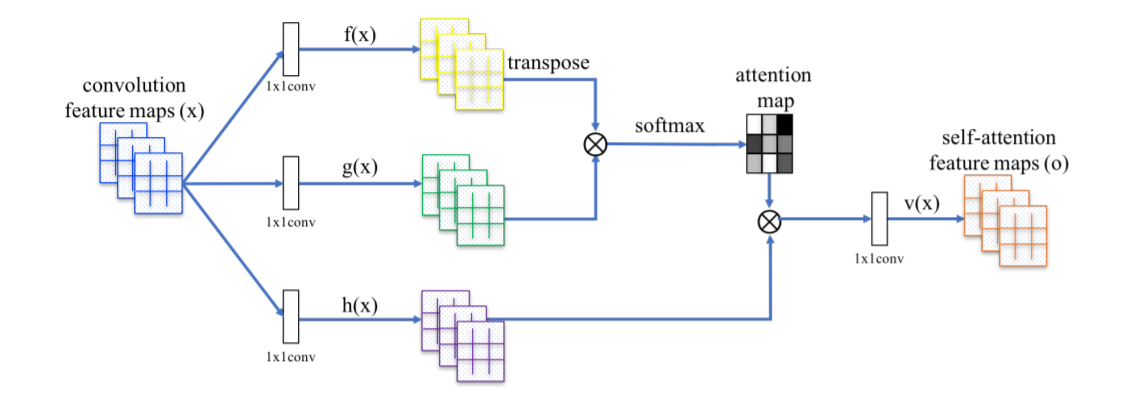
위의 구조에서 확인할 수 있듯이 softamax로 구해진 attention map을 $h$와 다시 결합을 하게 되는데 이때 사용되는 $h$ 역시 위에서의 $f$나 $g$처럼 파라미터인 $W_h$와의 곱을 통해 $h(x_i)=W_hx_i$식으로 구해진 값입니다. 이후 Attention map과 $h$를 결합하여 self-attention feature map을 뽑는 과정은 $o_j =v\left(\sum^N_{i=1}\beta_{j,i}h(x_i)\right)$라는 식으로 표현이 될 수 있겠습니다. 이때의 $v(x)$도 마찬가지로 $v(x_i)=W_vx_i$를 만족합니다.
Self-attention feature map들까지 얻게 된다면 이를 활용해 최종 결과 $y_i=\gamma o_i+x_i$를 도출하게 됩니다. 이때 $\gamma$의 역할은 scale parameter, 즉 점차적으로 non-local한 정보에 더 가중치를 주는 역할로 0으로 initialize해주게 됩니다.
SAGAN의 adversarial loss function은 다음과 같습니다. \(\mathit{L}_D=-\mathbb{E}_{(x,y)\sim p_{data}}\left[\min(0,-1+D(x,y))\right] -\mathbb{E}_{z\sim p_z,\; y\sim p_{data}}\left[\min(0,-1-D(G(z),y))\right] \\ \mathit{L}_D=-\mathbb{E}_{z\sim p_z,\; y\sim p_{data}}D(G(z),y)\)
식을 보시면 generator와 discriminator 모두 attention module이 적용되었음을 확인할 수 있으며 hinge version의 adversarial loss가 활용되었음을 알 수 있습니다.
2-2. Methods to stabilize the training
이전 모델들의 경우 GAN의 training 과정에서 안정적이지 못하거나 효율적이지 못한 경우들이 있었습니다. 이에 대한 해결책으로 SAGAN에서는 spectral normalization(이하 SN)과 two-timescale update rule(이하 TTUR)을 사용하게 됩니다.
먼저 SN의 경우 ‘Spectral normalization for generative adversarial networks’라는 논문에서 소개되었는데 discriminator의 Lipschitz 상수를 제한하여 gradient explode나 mode collapse를 막기 위해 사용되었으며 다른 테크닉들과는 다르게 추가적인 하이퍼파라미터 튜닝이 필요하지 않고 계산적인 비용이 상대적으로 적은 장점도 있어 채택되었습니다. 본 논문은 더 나아가 이 normalization 방법을 discriminator뿐 아니라 generator에도 적용하였습니다. 저자는 generator에서 SN이 파라미터 증가의 정도를 방지하고 비정상적인 gradients를 막을 수 있다고 설명합니다. 따라서 generator와 discriminator 모두에 SN을 적용하므로써 계산적인 비용을 줄이고 보다 안정적인 학습을 진행할 수 있었습니다.
TTUR의 경우 이전 논문들에서 discriminator에서의 regularization으로 인하여 GAN의 학습 과정이 느려지는 경우가 있었고 이를 해결하기 위하여 도입된 방법입니다. 이 방법은 generator와 discriminator의 학습속도를 다르게 하는 것으로 본 논문은 하나의 generator step과 비교하여 적은 discriminator step을 사용하여 더 좋은 결과를 도출해냈습니다. 그 결과에 대해서는 실험 및 결과 부분에서 좀 더 다뤄보겠습니다.
3. Experiment and Results
SAGAN 논문에서 결과적인 척도로 사용한 값들은 Inception Score(IS)와 Frechet Inception Distance(FID) 두 가지 지표입니다.
- Inception Score의 경우 conditional 클래스 분포와 marginal 클래스 분포간의 KL divergence를 구하는 것으로 높을수록 좋은 이미지 퀄리티를 보여준다고 해석할 수 있겠습니다. 식으로 표현하면 아래와 같습니다.
\(IS = exp(\mathbb E_x \mathbf{KL}(p(y|x) \lVert p(y)))\)
- FID의 경우 generate된 이미지와 실제 이미지 사이의 Wasserstein-2 distance를 구하는 방법으로 아래와 같은 식으로 표현이 됩니다. FID는 IS와는 다르게 낮을수록 좋은 이미지 퀄리티를 가지고 있다고 볼 수 있겠습니다.
3.1 Evaluating stabilization techniques
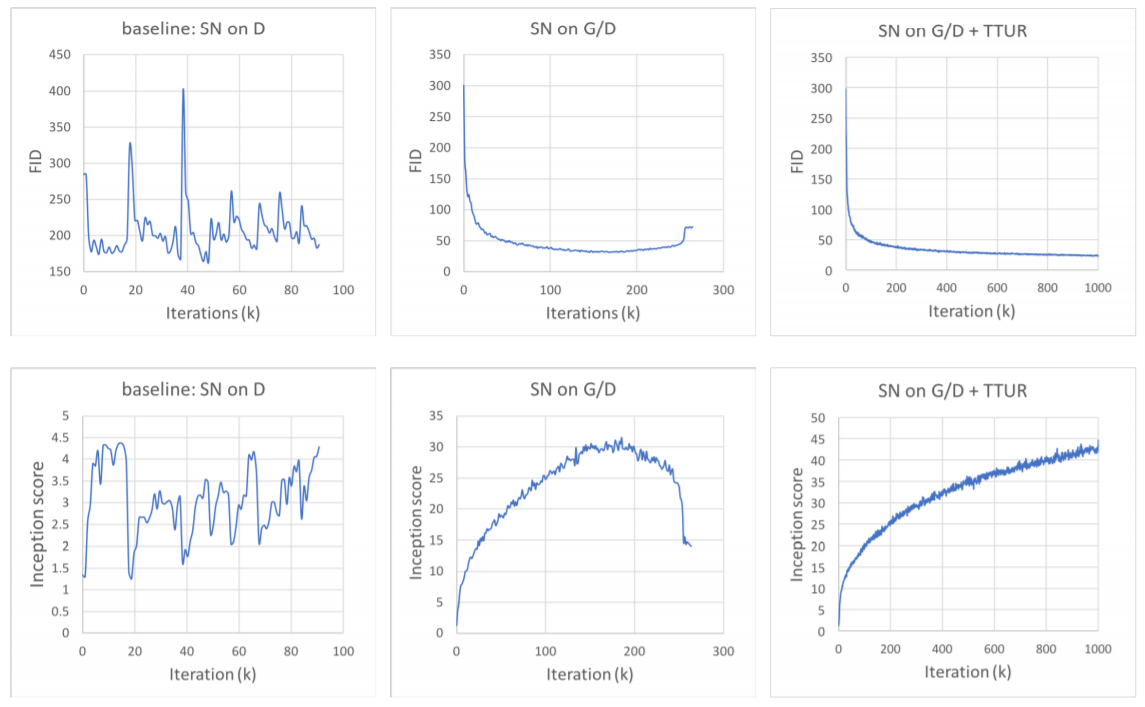

그림 3과 그림 4는 각각 SN과 TTUR의 적용에 따른 결과 그래프와 결과 이미지입니다. SN을 discriminator뿐만 아니라 generator에서도 사용하면서 TTUR을 적용하는 것이 가장 성능이 좋다는 것을 그래프와 이미지 결과물을 통해 확인할 수 있었습니다. SN을 discriminator에만 적용했을때 확실히 더 안정적인 결과를 보여주었고 TTUR을 추가했을시에는 더욱 지속적인 개선을 보여주었습니다.
3.2 Self-attention mechanism

두번째 실험은 self-attention을 사용했을때 일반적인 residual block을 사용했을때와 비교해서 어느 정도의 성과가 있는지 알아보는 것이었습니다. 표 1에서 확인할 수 있듯이 self-attention 모델을 사용하는 것이 residual block을 사용했을 때보다 낮은 FID, 높은 IS를 보여주어 더 좋은 퀄리티의 이미지를 만든다는 것을 확인할 수 있었고 특히 middle-to-high level feature이라고 할 수 있는 $32 \times 32, 64 \times 64$이미지, 즉 $feat_{32}, feat_{64}$에서 더 좋은 결과를 보여주었습니다. 높은 level의 feature에서 더 좋은 성능을 보이는 것은 self-attention이 더 큰 feature map에서 더 많은 정보들을 바탕으로 선택이 이루어지기 때문이라고 저자는 밝히고 있습니다.
3.3 Comparison with the SOTA

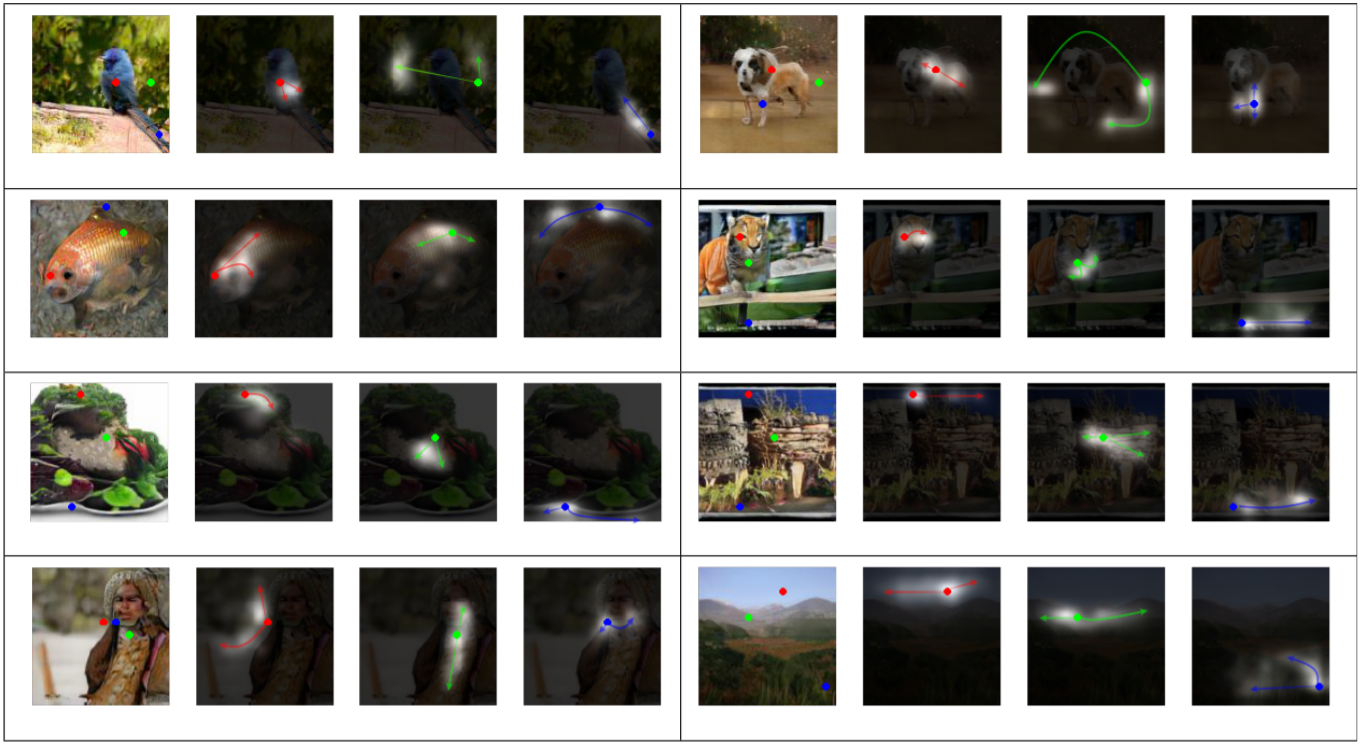
다른 모델들과의 성능 비교를 진행했을때에도 위의 표와 같이 state-of-the-art 모델들보다 좋은 성능을 보이는 것을 확인할 수 있었습니다. ImageNet으로 아래의 그림처럼 각각의 클래스들에 대한 평가를 진행해보았을때 결과를 보면 Saint Bernard나 goldfish처럼 좀 더 복잡한 기하학적 혹은 구조적 패턴을 가지는 경우 SAGAN이 월등히 좋은 모습을 보여주었습니다. 다만 valley이나 stone wall 등 구조적인 제약들이 거의 없는 이미지의 경우는 SOTA(Miyato&Koyama,2018)보다 다소 낮은 성능을 보여주었습니다.

