ADDA 논문 리뷰
1. Introduction
Dataset bias와 domain shift로 인하여 하나의 데이터셋으로 학습한 모델이 다른 데이터셋이 들어왔을때 생각만큼의 효과를 얻을 수 없는 경우가 많습니다. 이를 해결할 수 있는 방법으로 task-specific한 데이터셋을 통한 fine-tune이 있을 수 있겠지만 어렵고 비용이 많이 드는 작업입니다. 따라서 이번 논문의 토픽이라고 할 수 있는 domain adaptation(이하 DA)이 도입되었습니다. Domain shift의 영향을 최소화하기 위해 두 도메인을 common feature space에 맵핑하도록 DA가 적용되었다고 합니다.
Adversarial adaptation 방법은 도메인 차이의 distance를 domain discriminator에 대한 adversarial objective를 통해 최소화하도록 하는 방법입니다.
저자는 discriminative representation이 궁극적인 목표이기에 generative 모델링이 크게 필요하지 않다고 설명합니다. 따라서 본 논문의 ADDA 모델은 discriminative representation을 source labels를 통해 먼저 학습을 진행하고 domain adversarial loss를 통해 target encoder를 학습하게 됩니다.
2. Related Work
관련 내용들 혹은 이전 방법들을 간단하게만 정리하면 다음과 같습니다.
-
Maximum Mean Discrepancy(MMD) loss를 활용하는 방법
- 두 도메인의 평균 사이의 norm 구하는 방법입니다.
- Adversarial loss를 사용해서 domain shift를 줄이는 방법
- Source의 label은 구분하는 동시에 domains는 구분하지 못하도록 하는 방법입니다.
-
GAN
- Generator와 Discriminator를 활용하여 G의 경우 loss가 줄어들도록, D의 경우 loss가 증가하도록 학습이 되어 최종적으로 구분실제와 비슷하도록 이미지가 생성되는 모델입니다.
- 자세한 것은 본 논문의 링크를 참고 바랍니다. GAN논문
-
BiGAN
-
inverse mapping을 학습
-
자세한 것은 본 논문의 링크를 참고 바랍니다. BiGAN논문
-
-
CGAN
- GAN의 확장된 모델로서 추가적인 정보를 담은 vector가 input으로 들어가게 됩니다.
- 자세한 것은 본 논문의 링크를 참고 바랍니다. CGAN논문
-
CoGAN
- 두 개의 GAN을 각각 source와 target 이미지들로 학습시켜 domain transfer를 진행시키는 모델입니다.
- 자세한 것은 본 논문의 링크를 참고 바랍니다. CoGAN논문
관련 내용들은 링크를 첨부하오니 관심이 있으시다면 해당 논문들을 참고바랍니다. 본 논문은 위의 관련 내용들의 흐름에 따라 만들어진 모델이라고 할 수 있겠습니다. 이전의 CoGAN과의 차이점을 본 논문에서는 이미지 분포에 대한 모델링이 크게 필요하지 않다는 것이라고 소개하고 있으며 discriminative approach를 통해 실현하였습니다.
3. Generalized Adversarial Adaptation
-
Source and target
-
Source image $X_s$, Source labels $Y_s$, Source domain distribution $p_s(x,y)$, Source mapping $M_s$, Source classifier $C_s$
-
Target image $X_t$, No target labels, Target domain distribution $p_t(x,y)$, Target mapping $M_t$, Target classifier $C_t$
-
Adversarial adaptive 방법의 목표는 source와 target의 mapping, 즉 $M_s$와 $M_t$를 정형화하면서 $M_s\left(X_s\right)$와 $M_t\left(X_t\right)$의 거리를 좁혀주는 것입니다. 그리고 이를 만족하게 된다면 classifier의 경우에는 $C_s$가 그대로 target representations에 사용되어도 괜찮아질 것입니다. 즉, $C_t$를 따로 학습할 필요없이 $C=C_t=C_s$를 만족하게 됩니다.
Domain discriminator(이하 D)는 들어온 값이 source의 도메인을 가지는지 혹은 target의 도메인을 가지는지 판별해주는 역할을 합니다. D는 standard supervised loss에 의해서 최적화됨을 알 수 있습니다.
\[\mathcal{L}_{adv_D}\left(X_s, X_t, M_s, M_t\right)= \\ - \mathbb{E}_{x_s \sim X_s}\left[\log D(M_s(x_s))\right] - \mathbb{E}_{x_t \sim X_t}\left[\log (1-D(M_t(x_t)))\right]\]$M_s$와 $M_t$의 최적화의 경우 제한된 adversarial objective에 의해 진행됩니다.
\[\min_{D}\mathcal{L}_{adv_D}\left(X_s, X_t, M_s, M_t\right) \\ \min_{M_s, M_t}\mathcal{L}_{adv_M}\left(X_s, X_t, D\right) \\ s.t. \; \psi(M_s, M_t)\]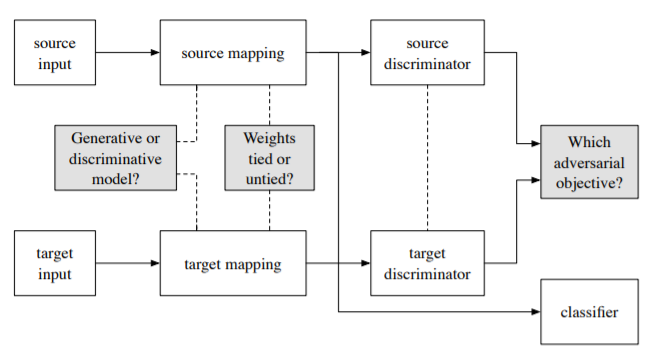
3-1. Source and target mapping
우선적으로 target label이 없는 상황이기 때문에 맵핑 과정을 parameterization 할 필요가 있습니다.
Parameterization과정이 source에 대해서 끝나게 된다면 어떻게 $M_t$를 parametrize할지 정해야 합니다. 각 레이어의 파라미터를 $M^l_s$와 $M^l_t$로 표현한다면 source와 target의 layerwise equality를 진행할 수 있는데 weight sharing을 통해 그 과정을 진행할 수 있습니다. 이전의 방법들은 대다수가 source와 target의 일정한 맵핑을 강조했지만 이 방법은 같은 네트워크로 서로 다른 도메인의 이미지를 처리해야하므로 최적화의 문제가 생길 수도 있습니다. 따라서 unshared weights(전체적 혹은 부분적)를 사용하는 방법이 대두되었다고 합니다.
3-2. Adversarial losses
$M_t$의 parametrization까지 결정하게 된다면 adversarial loss를 도입하여 실제 맵핑을 학습하게 됩니다. 이때 loss는 여러가지가 활용될 수 있는데 본 논문은 ‘GAN loss function’이라고 부르는 loss함수를 사용하였습니다. 이때의 식은 다음과 같습니다. \(\mathcal{L}_{adv_M}\left(X_s, X_t, D\right)= - \mathbb{E}_{x_t \sim X_t}\left[\log D(M_t(x_t))\right]\)
4. Adversarial Discriminative Domain Adaptation
모델을 구성하기 위해서 세 가지 중요한 선택사항이 있다고 합니다.
- Generative와 Discriminative 중 어떠한 것을 베이스로 선택할 것인가
- Weights를 공유할 것인가
- 어떤 loss를 사용할 것인가
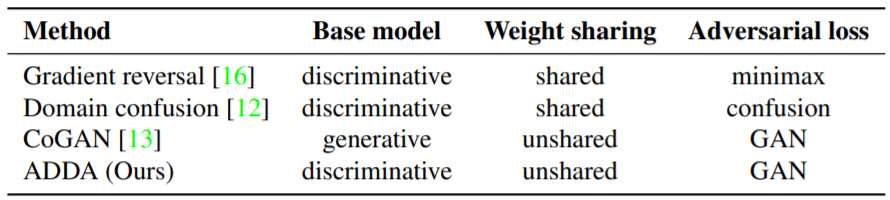
이 중 본 논문에서는 ‘Disriminative를 바탕으로 하는 모델, Unshared weights, standard GAN loss’ 이 세 가지를 선택하였습니다.
이 선택의 배경으로 저자는 이렇게 설명하고 있습니다.
- Generate에 사용되는 많은 파라미터들이 discriminative adaptation 과정과 무관한 경우가 많기 때문에 선택을 하였으며 실제로도 이전의 adversarial adaptive 방법들이 discriminative를 기반으로 둔 모델을 채택한 경우가 많았다고 합니다.
- Unshared weights를 사용하는 것이 더 많은 특정 domain에 대한 특징추출을 더 잘 학습하게 해주어 좀 더 유연성 있는 학습을 할 수 있도록 합니다. 다만 unshared weights를 사용하기는 하지만 target의 label이 없는 unsupervised한 학습이기 때문에 pre-trained된 source 모델을 initialization으로 사용하다고 합니다.
- Loss에 대한 설명은 3-2를 참고하시면 될꺼 같습니다.
최종적인 unconstrained optimization식은 아래와 같습니다. $$ \min_{M_s, C} \mathcal{L}{cls}(X_s, Y_s)= -\mathbb{E}{(x_s,y_s)\sim(X_s,Y_s)}\sum^K_{k=1}1_{[k=y_s]} \log C(M_s(x_s))\
\min_D \mathcal{L}_{adv_D}\left(X_s, X_t, M_s, M_t\right)=
- \mathbb{E}{x_s \sim X_s}\left[\log D(M_s(x_s))\right] - \mathbb{E}{x_t \sim X_t}\left[\log (1-D(M_t(x_t)))\right]
\min_{M_s,M_t}\mathcal{L}{adv_M}\left(X_s, X_t, D\right)= - \mathbb{E}{x_t \sim X_t}\left[\log D(M_t(x_t))\right] $$ 먼저 $\mathcal{L}{cls}$를 labelling된 source 데이터를 통하여 최적화하고 이후 $M_S$는 고정하는 동시에 $M_t$를 학습하면서 $\mathcal{L}{adv_D}$와 $\mathcal{L}_{adv_M}$을 최적화합니다.
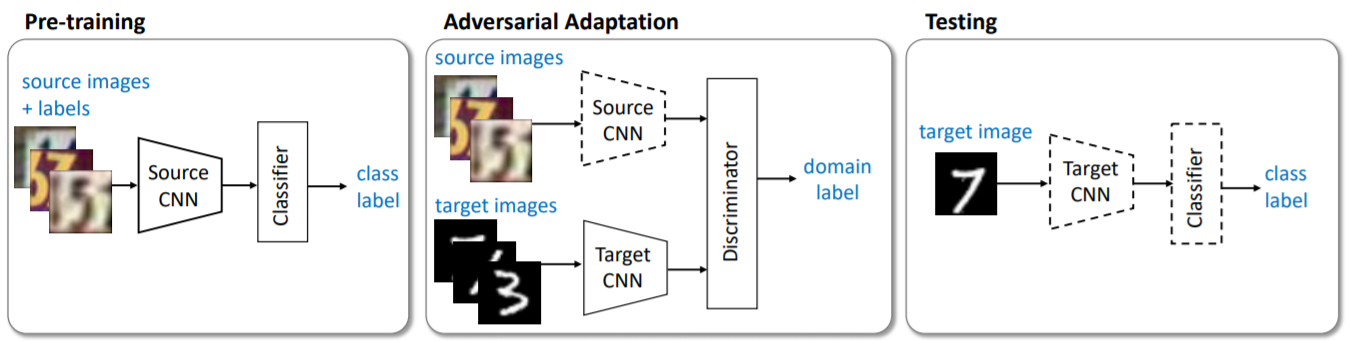
간단하게 구조를 보면 Source 도메인 데이터를 활용하여 source representation과 classifier를 학습하고 source representation을 고정하면서 adversarial loss를 통해 target representation을 학습한 후 target representation과 기존의 classifier로 test과정을 진행하는 모습을 확인할 수 있었습니다.
5. Experiments
위의 모델의 결과를 확인하기 위하여 본 논문은 MNIST, SVHN, USPS 데이터를 활용하는 실험과 NYUD 데이터를 활용하는 실험으로 DA를 진행하였습니다.

5-1. MNIST, USPS and SVHN digit datasets
첫번째 실험의 경우 MNIST를 USPS로, USPS를 MNIST로, SVHN은 MNIST로 adaptation을 하는 과정을 진행하였습니다. 이때 기본적인 설정은 LeNet구조, 3개의 fully-connected layers, 이중 두 개의 layers는 500개의 hidden units with ReLU를 가지도록 설정하였다고 합니다. 그 결과는 아래의 사진과 표에 나타납니다. 보시다시피 다른 방법들보다 ADDA가 좀 더 높은 점수로 잘 adaptation이 이루어지는것을 확인할 수 있습니다.

5-2. Modality adaptation
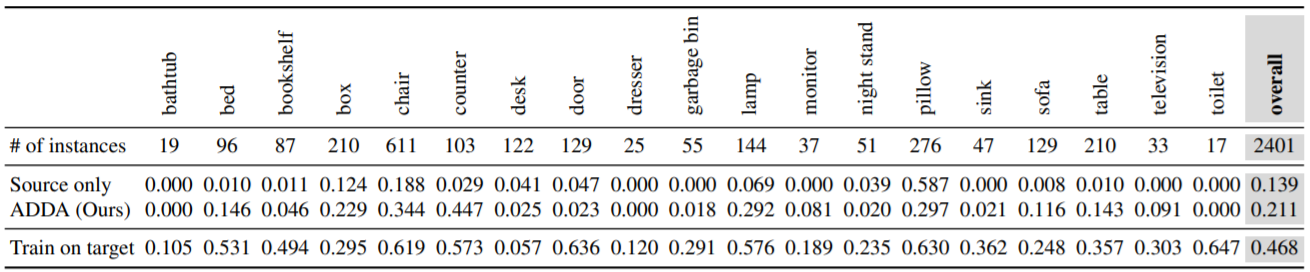
두번째 실험의 경우 19개의 클래스를 가지는 1449개의 이미지 데이터셋인 NYU depth 데이터셋의 RGB이미지와 HHA 이미지를 사용하여 실험을 진행하였습니다. 이 실험에서는 ImageNet으로 학습된 VGG-16구조로 source domain을 batch size 128, 20000번의 iterations를 통해 fine-tuned 하였고 3개의 추가된 fully-connected layers를 통하여 discriminate하는 과정을 거쳤습니다. 그 결과값들은 아래의 사진, 표와 같습니다. 그 결과 classification의 정확도가 대체적으로 높아짐을 확인할 수 있었습니다. 물론 모든 class에 대해서 정확도가 높아진 것은 아닙니다. 다만 전반적으로 모든 class들에 대해서 정확도가 높아졌다고 밝히고 있습니다.